La force centrifuge

Qu’est-ce que la force centrifuge ?

La force dite centrifuge, s’applique à un objet en rotation. Cet effort centrifuge est une composante de force qui tend à éloigner un objet de son centre de rotation. L’appellation de « force » fait souvent débat car la force centrifuge est parfois assimilée à une force fictive. Je détaillerai dans cet article comment la calculer et l’interpréter.

Cas d’application

On peut ressentir l’effet de cette force dans les manèges des parcs d’attraction. Prenons l’exemple de la Tour du Prater dans le Parc d’attraction le Prater de Vienne. Lorsque le manège tourne, la chaise du visiteur exerce une force radiale sur la corde qui la retient. On remarque que plus le manège tourne vite, plus la corde qui retient la chaise se tend à l’horizontal. Sans avoir posé le problème, on peut déjà supposer que la force centrifuge dépend de la vitesse de rotation. Seulement, elle ne dépend pas que de cela… Regardons ensemble son expression.

Calculer la force centrifuge

Commençons par poser notre problème. Je m’intéresse à un solide en rotation. Notons $R$ $(O,\vec{e_x},\vec{e_y},\vec{e_z})$ un repère fixe dans un référentiel Galiléen et je définis un axe $Z$ tel que $Z = (O,\vec{e_z})$ .

Le solide $M$ est entraîné en rotation par rapport à l’axe $Z$ par l’intermédiaire d’une barre rigide fixée au point $O$ . Par ailleurs, je définis le repère $R' (O,\overrightarrow{e_x_'},\overrightarrow{e_y_'},\overrightarrow{e_z_'})$ tel que $R'$ est en rotation par rapport à $R$ autour de l’axe $Z$ . L’angle de cette rotation est $\theta(t) = ( \overrightarrow{e_x}, \overrightarrow{e_x_'} )$ . Pour finir, j’attache mon solide $M$ au repère $R'$ .

Créer le repère $R'$ me permet d’avoir une expression simple de la composante radiale de mon solide $M$ et ce, pour tout instant $t$ . Je peux alors noter que $\overrightarrow{OM} \cdot \overrightarrow{e_x_'} = r$ .

Mon objectif en modélisant le problème de cette manière est de calculer l’accélération du solide $M$ suivant le vecteur $\vec{e_x_'}$ . Ensuite, j’appliquerai le principe fondamental de la dynamique (PFD) à ce solide et je m’intéresserai uniquement au terme suivant ce vecteur.

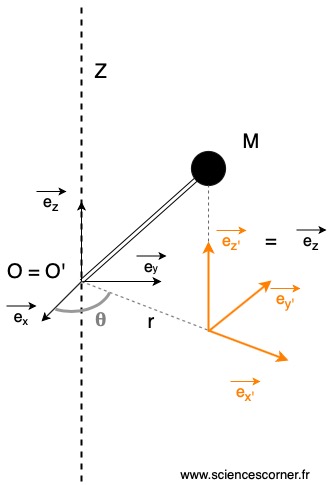
Accélération du solide M

C’est parti. Je calcule dans un premier temps la vitesse instantanée de $M$ dans $R$ :

$\overrightarrow{\frac{d OM}{dt}\arrowvert_R} = \overrightarrow{\frac{d OM}{dt}\arrowvert_R_'} + \overrightarrow{\Omega_R_'/R} \wedge \overrightarrow{OM}$

Avec $\overrightarrow{\Omega_R_'/R} = \dot{\theta} \enspace\vec{e_z}$ la vitesse de rotation de $R'$ par rapport à $R$ .

$\overrightarrow{\frac{d OM}{dt}\arrowvert_R_'} = \vec{0}$ car la barre est rigide donc sa longueur ne dépend pas du temps.

On a alors :

$\begin{align*}\overrightarrow{\frac{d OM}{dt}\arrowvert_R} &= \overrightarrow{\Omega_R_'/R} \wedge \overrightarrow{OM}\\&= \dot{\theta} \vec{e_z} \wedge r \overrightarrow{e_x_'} \\&= r\cdot\dot{\theta} \enspace \overrightarrow{e_y_'} \end{algin*}$

Je dérive ensuite mon vecteur vitesse précédemment obtenu pour déterminer l’accélération en $M$ :

$\begin{align*}\overrightarrow{\frac{d^2 OM}{dt^2}\arrowvert_R} &= \overrightarrow{\frac{d (r\cdot\dot{\theta})}{dt}} \enspace \overrightarrow{e_{y'}} + r\cdot\dot{\theta} \cdot \frac{d \overrightarrow{e_{y'}}}{dt}\arrowvert_R \\&= r\cdot\ddot{\theta} \enspace \overrightarrow{e_{y'}} + r\cdot\dot{\theta} \cdot ( \overrightarrow{\Omega_R_'/R} \wedge \enspace \overrightarrow{e_{y'}} )\\&= r\cdot\ddot{\theta} \enspace \overrightarrow{e_{y'}} - r\cdot\dot{\theta}^2 \enspace \overrightarrow{e_{x'}}\end{algin*}$

Nous y sommes presque. Nous avons déterminé la composante radiale de l’accélération du point $M : \overrightarrow{\frac{d^2 OM}{dt^2}\arrowvert_R} \cdot \overrightarrow{e_{x'}} = - r\cdot\dot{\theta}^2$ . Il ne nous reste plus qu’à appliquer le PFD sur $M$ .

Lien entre la mécanique et la cinématique

J’isole $M$ et je fais le bilan des actions mécaniques. J’émets l’hypothèse que les forces de frottement dans l’air sont négligeables par rapport aux autres forces en jeux.
$\vec{T} = T_x \enspace \overrightarrow{e_{x'}} + T_z \enspace \overrightarrow{e_{z}}$ : Tension de la barre sur le solide $M$ .
$\vec{P} = P \enspace \overrightarrow{e_{z}}$ : Poids du solide.

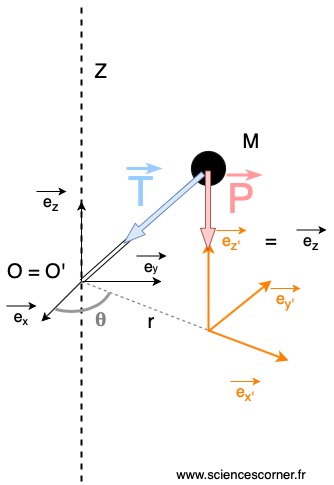
Représentation des efforts sur le schéma de principe — *Représentation des efforts*

Soit $m$ la masse du solide $M$
J’applique le théorème de la résultante sur $M$ :

$\sum \overrightarrow{F_{ext \rightarrow M}} = m \cdot \overrightarrow{\frac{d^2 OM}{dt^2}\arrowvert_R}$

Comme je disais précédement, on s’intéresse à la composante radiale. On note alors :

$\begin{align*}( \vec{T} + \vec{P} ) \cdot \overrightarrow{e_{x'}} &= ( m \cdot \overrightarrow{\frac{d^2 OM}{dt^2}\arrowvert_R} ) \cdot \overrightarrow{e_{x'}} \\&= - \enspace m \cdot r\cdot\dot{\theta}^2.\end{algin*}$

Par ailleurs, le terme à gauche de l’équation vaut :

$( \vec{T} + \vec{P} ) \cdot \overrightarrow{e_{x'}} = T_x$

On y est presque… Nous avons déterminé l’action radiale qu’exerce la barre sur le solide $M$ . Le principe d’action réaction implique que la force du solide $M$ sur la barre est égale à l’opposée de la force qu’exerce la barre sur le solide $M$ . Notons alors :

$F_c = - \enspace T_x$

On y est, l’effort radial qu’exerce le solide sur la barre est :

$\boxed{ F_c = m \cdot r\cdot\dot{\theta}^2}$

Que nous dit cette expression ?

Nous avons déterminé l’expression mathématique de la composante radiale de la force exercée par le solide $M$ sur la barre :

$\boxed{ F_c = m \cdot r\cdot\dot{\theta}^2}$

Cette composante de force est appellée force centrifuge. Voyons ce que nous enseigne cette expression.

Toutes les composantes de cette force sont positives donc 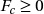$F_c \geq 0$ . Ceci implique que la force centrifuge amène le solide M à s’éloigner du centre de rotation.
Pour faire varier la valeur de cette force, il est possible de jouer sur trois facteurs. La masse du solide, la distance du solide par rapport à son axe de rotation et sur la vitesse de rotation du solide. Remarquons que la vitesse de rotation est élevée au carré. Ainsi, une variation de vitesse de rotation influera plus sur la valeur de la force qu’une variation de masse ou une variation de distance.

Pour aller plus loin…

Au début de l’article, j’ai dit que la force centrifuge pouvait être assimilée à une force fictive, point sur lequel je voudrais m’arrêter un instant.

Prenons l’exemple de notre cas précédent. Le solide $M$ est accroché à une barre qui entraîne ce solide en rotation autour de l’axe $Z$ . Supposons qu’à l’instant $t$ il est accroché à la barre et qu’à l’instant $t+1$ il se détache de la barre. Qu’en est-il du bilan des actions mécaniques sur $M$ ? La seule force s’appliquant au solide $M$ est son poids $\vec{P} = P \enspace \overrightarrow{e_{z}}$ . Ainsi, le terme $F_c$ précédemment calculé n’existe pas.

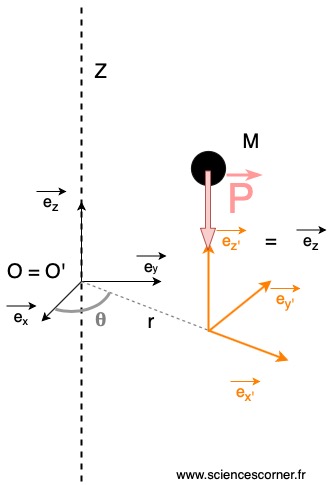
Pourtant, on se doute qu’aux instants suivant l’instant $t+1$ , le solide va se déplacer dans l’espace avec entre autre une composante radiale. C’est la conséquence de l’inertie du solide mais ceci fera l’objet d’un autre article.

Le mot de la fin

En résumé, la force centrifuge est une force radiale exercée par un solide en rotation autour d’un axe. La valeur de cette force dépend de la masse du solide, de sa distance par rapport à l’axe de rotation et de sa vitesse de rotation.

J’espère que maintenant tu comprends mieux ce qu’est la force centrifuge, et que cet article t’a donné envie d’en connaître encore plus sur les modèles qui nous entourent.

Connais tu des exemples où la force centrifuge s’applique ? Partages les nous en laissant un commentaire. Je t’invite également à t’abonner à la Newsletter afin de ne manquer aucun nouveaux sujets.

À bientôt !

2 thoughts on “La force centrifuge”

Jean-Marc dit :

29 novembre 2023 à 10 h 54 min

Bonjour, merci pour ces longs calculs!
mais je suis surpris par l’équation finale qui établit que FC=m x r x v2 … ?
N’est ce pas m x v2/r ?

Intuitvement on s’attend d’ailleurs qu’à vitesse et masse constantes, la FC soit plus faible avec un long rayon de virage qu’un court (donc v2/r et pas v2 x r )

Merci!
JiM

Répondre
1. Harry dit :
  
  4 décembre 2023 à 22 h 26 min
  
  Bonjour Jean-Marc,
  Merci pour ton intérêt pour cet article. Je répondrai à ta question en 3 étapes.
  Tout d’abord, je précise que la vitesse en jeu est une vitesse de rotation et pas une vitesse linéaire « V ».
  
  Ensuite, il est à mon avis plus facile de ressentir l’influence du rayon « r » sur la force centrifuge en regardant un lancé de disque. En effet on peut voir que le lanceur tient le disque le plus éloigné de son corps avant de le lâcher. Dans le cas où le lanceur libérerait le disque proche de son corps, on peut s’attendre à ce que le disque parte moins loins.
  
  Pour finir, je te propose de répondre à ta question en vérifiant que l’équation est bien homogène à une force.
  Prenons l’exemple de la force de pesanteur. Elle s’écrit Fp = m*g, où « m » est la masse en [kg] et « g » l’accélération de la pesanteur [m/s^2]. Donc l’unité de la force de pesanteur, et par conséquent d’une force est homogène à des [kg*m/s^2].
  Revenons maintenant à notre équation. Nous avons noté que la force centrifuge s’écrit Fc = m*R*W^2, où « m » est la masse en [kg], « R » la distance par rapport à l’axe de rotation en [m] et « W » est la vitesse de rotation en [rad/s].
  Par conséquent, notre expression de la force centrifuge est homogène à des [kg*m*(rad/s)^2]. Cependant il faut savoir que les radians ne sont pas à proprement dit une dimension. Finalement, la dimension de la force centrifuge dans cet article est [ kg*m/s^2], donc bien la dimension d’une force.
  
  J’espère que ma réponse à ton commentaire t’aura apportée des éléments de réponse.
  Bonne journée !
  
  Répondre

Qu’est-ce que la force centrifuge ?

Cas d’application

Calculer la force centrifuge

Accélération du solide M

Lien entre la mécanique et la cinématique

Que nous dit cette expression ?

Pour aller plus loin…

Le mot de la fin

1 fiche de cours offerte !

2 thoughts on “La force centrifuge”

Laisser un commentaire Annuler la réponse

Le mur du son

Le paradoxe de Levinthal

Le clonage

La corrosion du métal en milieu aqueux

L’ATP et l’énergie musculaire

Le feu de saint-Elme

Réseaux sociaux

Informations

S'abonner à la Newsletter

Informations

Catégories

À voir sur le Web