Le paradoxe de Levinthal

Je t’invite dans cet article à descendre avec moi dans l’univers des macromolécules de la taille de quelques Angströms. L’échelle que nous abordons ici est telle que vaut . La macromolécule en jeu dans le paradoxe de Levinthal est la protéine. Afin de connaître l’environnement qui entoure la protéine, je partirai du niveau de l’organisme vivant et je cheminerai avec toi jusqu’au niveau moléculaire. Commençons notre visite dans le monde du très petit !

De l’organisme vivant à la molécule

Les organismes vivants sont présents tout autour de nous. Ils peuvent être visibles par l’oeil humain ou par l’intermédiaire de microscope ou autres instruments du même genre. Une plante, un petit poisson ou un humain sont des organismes vivants. À une autre échelle, une bactérie est aussi un organisme vivant.

Un organisme vivant est composé d’une ou de plusieurs cellules vivantes. Chaque cellule a sa mission dans ce système vivant qui peut être plus ou moins complexe. Une cellule peut par exemple produire des hormones, stocker de l’énergie et bien d’autres fonctions. Une cellule est une magnifique entité vivante et complexe sur laquelle je ne vais pas m’étendre ici. Je souhaite surtout t’amener à t’intéresser à cette usine qui compose une cellule.

De la cellule à la protéine

Il existe deux grandes classes de cellule, les cellules eucaryotes et procaryotes. Ces deux types de cellules se distinguent par leurs tailles, les organites qui la composent mais aussi par leurs structures internes. Les cellules procaryotes ont une structure plus simple que les eucaryotes. On retrouve parmi les cellules procaryotes les bactéries alors que les eucaryotes comprennent les champignons, les protistes, les plantes et les animaux.

Malgré cet écart structurel entre ces deux types de cellule, nous retrouvons des éléments communs aux deux classes. Toutes deux sont constituées d’un code génétique commun, d’une membrane plasmique et de ribosomes.

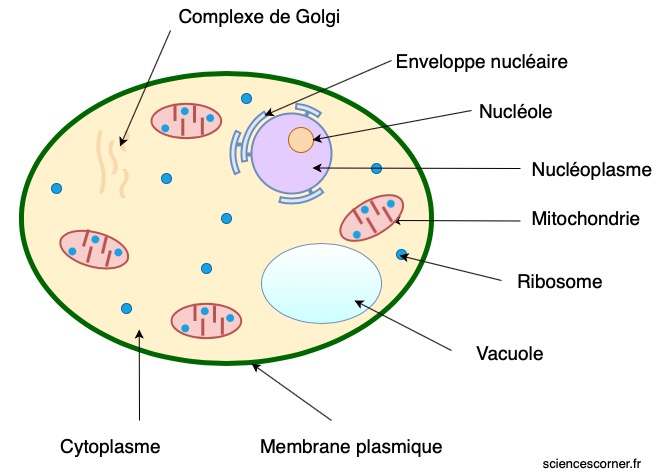
Il y a beaucoup d’activité dans une cellule. Comme je l’ai amplement répété, la cellule est vivante. Elle peut donc se nourrir, croître et se développer. Ainsi, la cellule doit pouvoir puiser de l’énergie à l’extérieur de sa membrane et la stocker en interne. Elle doit aussi être en mesure d’exploiter cette énergie qu’elle a de stocké en elle pour fabriquer des éléments nécessaires à sa survie, par exemple produire des protéines via les ribosomes.

Contexte du paradoxe de Levinthal

Une protéine est une macromolécule dont la taille est de l’ordre du Angströms. Il peut y avoir plusieurs protéines dans une cellule et chaque protéine a un rôle différent à jouer pour le bon fonctionnement de la cellule. Imagine une usine automobile avec des chaînes d’assemblage. Afin de fabriquer une voiture par exemple, il faut des instructions et des ouvriers. Et bien, dans la cellule, on peut imaginer que les informations nécessaires à la fabrication sont les acides aminés et que les protéines sont les ouvriers.

Nous avons presque atteint le paradoxe de Levinthal. Focalisons maintenant notre expédition sur la fabrication d’une protéine. Les protéines en elles mêmes sont des successions d’acides aminés reliés par des liaisons peptidiques. Elles sont synthétisées dans les ribosomes lorsque le besoin de ces protéines est remonté par le noyau.

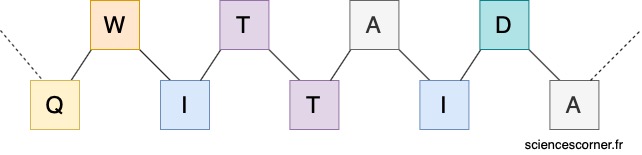
Afin d’être fonctionnelle, la protéine doit se replier sur elle même jusqu’à atteindre une forme 3D appelée structure native. C’est précisément sur ce processus de repliement que repose le paradoxe de Levinthal.

Un côté surprenant des cellules est que, bien que complexe, elle est régie par des processus physiques aléatoires. Les molécules comprenant une cellule sont mis en mouvement de manière aléatoire par l’énergie thermique qu’elles ont emmagasiné par le milieu environnant. La cellule va alors exploiter ces mouvements aléatoires et les orienter dans le sens qui lui convient. Mais qu’en est-il du repliement de la protéine, est-il tout aussi aléatoire ?

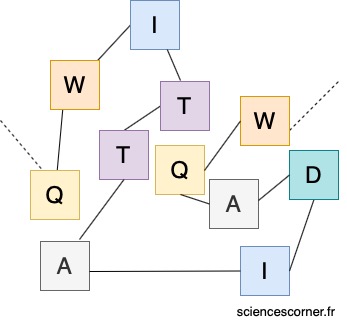
Le paradoxe de Levinthal

Le paradoxe de Levinthal montre que la recherche de la structure native d’une protéine par un processus aléatoire peut prendre énormément de temps. Pourtant, le repliement d’une protéine n’est l’affaire que d’une fraction de seconde.

Quel est l’ordre de grandeur de « énormément de temps » ?

Imaginons que le noyau d’une cellule demande la fabrication d’une petite protéine de acides aminés. Le nombre de conformation possible de cette protéine est égal à avec le nombre de structure possible pour chaque acide aminé, et le nombre d’acide aminé de la chaîne.

Qu’est-ce que la conformation d’un acide aminé ?

La conformation d’un acide aminé est sa représentation spatiale. Un acide aminé peut avoir plusieurs conformations possibles. Je ne m’étendrai pas ici sur les acides aminés, mais il est nécessaire que tu les visualises afin de comprendre la suite de l’explication. Prenons l’exemple de deux conformations, la forme et .

Un acide aminé, présent dans une protéine, comprend un atome centrale, le auquel est relié un groupe carboxyle , un groupe amine , un atome d’hydrogène et une chaîne latérale .

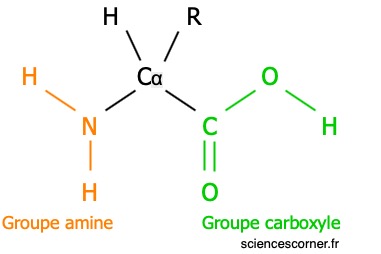
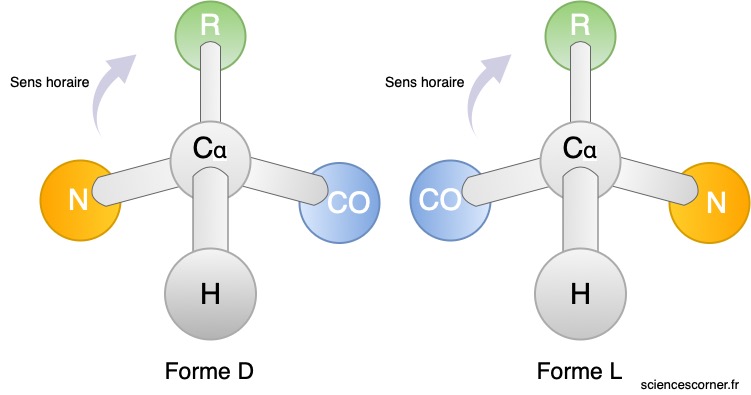
Toutefois, un acide aminé a une représentation tridimensionnelle. Ainsi, si on lit les molécules, autour de l’atome de , dans le sens horaire, et ce en regardant l’atome de carbone dans la direction de la liaison , on obtient dans l’ordre ou respectivement les formes et .

Considérons alors dans notre exemple qu’uniquement conformations sont possibles pour un acide aminé. Ainsi, la protéine peut se retrouver dans configurations différentes.

Maintenant, supposons que la protéine se replie de manière aléatoire et ce, avec un taux de repliement vers une nouvelle configuration de configurations par seconde, soit configurations par an. Une telle hypothèse implique que pour atteindre sa structure native, notre protéine prendrait années.

Que faut-il comprendre de ce résultat ?

Si le processus de repliement de la protéine est strictement aléatoire, alors il faudrait patienter des milliards d’années, voir beaucoup plus, pour obtenir une petite protéine. A l’échelle de la vie, cette durée n’est pas envisageable et, l’expérience du vivant qui nous entoure le confirme. En conséquence, le repliement d’une protéine n’est pas un processus strictement aléatoire. Ainsi, le paradoxe de Levinthal ne nous enseigne pas comment se replie une protéine mais, il nous apprend comment elle ne se replie pas, ce qui est une information toute aussi instructive dans la recherche.

Pour conclure

Le paradoxe de Levinthal nous montre que le processus de repliement d’une protéine n’est pas simplement aléatoire mais qu’il doit être dirigé. Toutefois des concepts sur le processus de repliement des protéines existent. Ils s’appuient entre autre sur le principe de « l’entonnoir de repliement ». Le repliement correct d’une protéine est très important. Une protéine mal repliée ne peut pas assurer sa fonction dans la cellule. En conséquence, cette cellule peut devenir une source de maladie tel que la maladie Creutzfeldt-Jakob chez l’homme.

Le repliement des protéines est un riche sujet que j’ai pris plaisir à étudier. Si toi aussi tu as aimé découvrir ce sujet et que tu as envi d’en connaître d’autres, inscris toi à la Newsletter et reste informé des nouveaux sujets sur Sciences Corner.

---

Pour aller plus loin, tu peux parcourir ces différentes ressources :

• Karp, G. (2018). Biologie cellulaire et moléculaire. De Boeck SUPERIEUR
• Laboratory of Chemical Physics, National Institute of Diabetes and Digestive and Kidney Diseases, Building 2, National Institutes of Health, Bethesda,MD 20892 (1992). Levinthal’s paradox. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC48166/pdf/pnas01075-0036.pdf
• Perrot, O. (2016, 11 Octobre). Cours Ifsi – Biologie fondamentale – la cellule (partie 1). Consulté le 28 Avril 2020 sur https://www.infirmiers.com/etudiants-en-ifsi/cours/cours-ifsi-biologie-fondamentale-la-cellule-partie-1.html
• Benhabilès, N. Thomas, A. Brasseur, R. (2000). Les mécanismes de repliement des protéines solubles. https://popups.uliege.be/1780-4507/index.php?id=17488&file=1&pid=15325