C’est l’évènement astronomique du moment ! Partout sur internet, on entend parler de la comète Neowise. Ce qui est fascinant avec cette comète, c’est qu’elle est visible à l’oeil nu. Seulement, il faut juste s’armer de courage pour pouvoir l’observer tôt, très tôt le matin… En effet, ce spectacle est visible avant le lever du soleil, vers 4h30 en France. Mais la passion dépasse les rêves ! J’ai donc réglé mon réveil afin de participer aussi à ce spectacle. Le réveil fût difficile mais bon, ce n’est pas le type d’évènement que l’on voit tous les jours.
D’ailleurs, pourquoi est-ce que ce type d’évènement est si peu fréquent ? Curieux de connaître la réponse, j’ai bouquiné sur le sujet et je te partage les réponses. Pour comprendre ce qu’il se passe, il faut s’intéresser aux lois de Kepler. D’où viennent ces lois et que disent-elles ? C’est ce que je t’explique dans cet article.
Le système solaire et les lois de Kepler
Tout d’abord, prenons un peu de recul et regardons dans quel environnement se situe notre planète. La Terre fait partie du système solaire. Le système solaire est le système planétaire pour lequel le soleil en est le centre. Dans le système solaire, différents corps célestes gravitent autour du soleil. Parmi ceux-ci, on retrouve les planètes et leurs satellites, les astéroïdes, les comètes et bien d’autres corps.
En regardant en arrière dans l’histoire, on constate que les trajectoires des corps célestes ont longtemps été étudiées par les astronomes de l’époque. Par exemple, vers le IVe siècle av J-C, selon Aristote, l’unique mouvement possible par un astre est un mouvement circulaire uniforme. Cependant, cette définition est contredite par les observations de Jupiter, Mars ou encore Vénus. En effet, les comparaisons entre leurs positions et celles des étoiles fixes montrent que les planètes semblent accélérer, freiner voir revenir en arrière. D’un autre côté, Ptolémée au IIe siècle, présente quant à lui dans son Almageste un système complexe dans lequel la trajectoire des planètes est un cercle et, le centre de ces cercles décrivent eux mêmes un cercle centré sur la Terre.
Il est important que tu saches qu’à cette période, la Terre était considérée comme le centre de l’univers. Alors, tous les astres célestes devaient, de ce fait, se mouvoir autour de la Terre. Toutefois, cette vision du Monde n’était pas partagée par tout le monde. Ainsi, en 1543, dans son livre De Revolutionibus, Copernic présente un tout autre système cette fois centré autour du Soleil. On parle alors de révolution copernicienne. Ceci dit, Copernic n’avait pas tout juste, il a fallu attendre d’autres astronomes pour préciser cette idée. Kepler fût l’un d’entre eux.

Après ce bref retour dans le temps, regardons ensemble ce que Kepler a découvert en observant le ciel.
1ère loi de Kepler : Loi des orbites
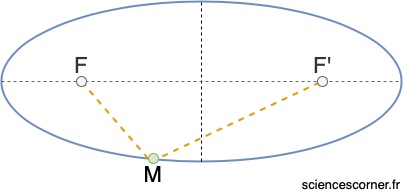
La première loi de Kepler, ou loi des orbites décrit la trajectoire parcourue par un astre en orbite. Elle nous dit que : ![]()
Allez, un petit rappel de géométrie si tu ne sais plus comment est définie un ellipse.
Une ellipse est une courbe plane fermée que l’on peut définir par la méthode du jardinier. Le procédé est le suivant : Soit ![]() et
et ![]() deux points distincts. L’ensemble des points
deux points distincts. L’ensemble des points ![]() tel que,
tel que, ![]() forment une ellipse de foyers
forment une ellipse de foyers ![]() et
et ![]() .
.
2ème loi de Kepler : Loi des aires
La deuxième loi de Kepler ou loi des aires dit que :![]() .
.
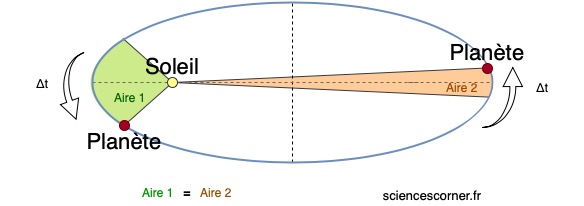
Remarquons une conséquence de cette loi sur le schéma ci-dessus. La longueur de la courbe parcourue par la planète à gauche de l’ellipse, est plus grande que lorsqu’elle la parcourt à droite de l’ellipse, dans un même intervalle de temps. Ce qui veut dire qu’au voisinage du Soleil, les planètes accélèrent puis ralentissent en s’y éloigant.
3ème loi de Kepler : Loi des périodes
La troisième loi relie la géométrie de l’ellipse parcourue par une planète, et le temps qu’elle prendra pour faire une révolution complète. Cette loi dit que : ![]()
![]()
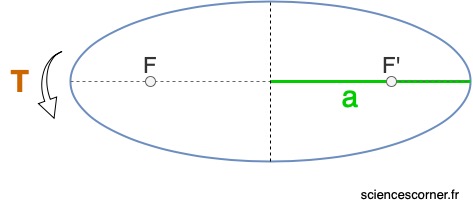
Pour la Terre, le demi-grand axe de son orbite vaut ![]() et sa période de révolution
et sa période de révolution ![]() environ.
environ.
Lois de Kepler et orbite de transfert de Hohmann
Lien entre lois de Kepler et orbites de transfert
Les lois de Kepler nous enseignent sur les trajectoires des astres, leurs vitesses et leurs périodes de révolution. Dans la nature cela fonctionne assez bien mais, est-ce qu’à partir de ces lois je peux moi aussi imaginer mettre des objets sur orbite ? Et bien oui, et c’est le cas de l’ISS ( International Space Station) qui est en orbite basse autour de la Terre.
Mettre en orbite un objet, par exemple autour de la Terre, demande une très grande précision. Un des procédés qui existe consiste à utiliser ce que l’on appelle des orbites de transfert. Le principe est assez simple mais très ingénieux, je t’explique.
L’orbite de transfert de Hohmann
Une orbite de transfert est une orbite intermédiaire entre une orbite de départ et une orbite d’arrivée. Ainsi, elle permet à un objet de s’approcher ou de s’éloigner de l’astre autour duquel il se meut.
L’orbite de transfert de Hohmann correspond à la trajectoire consommant le minimum d’énergie pour passer d’une orbite circulaire de rayon ![]() à une autre orbite circulaire de rayon
à une autre orbite circulaire de rayon ![]() . Prenons l’exemple d’un satellite artificiel autour de la Terre.
. Prenons l’exemple d’un satellite artificiel autour de la Terre.
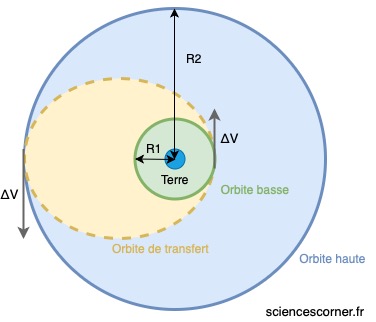
Tout d’abord, le satellite est placé en orbite basse de rayon ![]() grâce à un lanceur, par exemple Ariane 5. Ensuite, sur cette orbite basse, le satellite va accélérer tangentiellement à son orbite de rayon
grâce à un lanceur, par exemple Ariane 5. Ensuite, sur cette orbite basse, le satellite va accélérer tangentiellement à son orbite de rayon ![]() . Ceci aura pour conséquence de redéfinir une nouvelle orbite du satellite. Cette nouvelle orbite dite, orbite de transfert, est alors une ellipse. En choisissant intelligemment l’accélération donnée au satellite, on obtient que l’extrémité opposée de l’ellipse obtenue, est distante de la Terre de
. Ceci aura pour conséquence de redéfinir une nouvelle orbite du satellite. Cette nouvelle orbite dite, orbite de transfert, est alors une ellipse. En choisissant intelligemment l’accélération donnée au satellite, on obtient que l’extrémité opposée de l’ellipse obtenue, est distante de la Terre de ![]() . Pour finir, une fois que le satellite a atteint l’extrémité
. Pour finir, une fois que le satellite a atteint l’extrémité ![]() , il va à nouveau accélérer pour définir son orbite d’arrivée. Astucieux non?
, il va à nouveau accélérer pour définir son orbite d’arrivée. Astucieux non?
Ce qu’il faut retenir
La magnifique comète Neowise est un des nombreux astres qui gravite autour du soleil. Comme tous ses confrères, elle n’échappe pas aux trois lois de Kepler. Son excentricité étant plus grande que celle de la Terre, la forme de son ellipse est alors plus étirée que l’ellipse de la Terre. Ceci explique notamment pourquoi son passage à proximité de la Terre est peu fréquent.
Connaisseur de tous ces principes qui entourent notre belle planète, nous sommes aussi en mesure de mettre sur orbite des satellites qui sont devenus aujourd’hui des outils indispensables dans notre quotidien.
Maintenant que toi aussi tu sais pourquoi les comètes sont si peu souvent observables depuis la Terre, il ne te reste plus qu’une chose à faire, régler ton réveil et profiter du spectacle de l’univers avant la prochaine scène !
Tu as pris de superbes photos de la comète Neowise ? Magnifique ! partage les nous sur instagram en identifiant @sciencescorner.
Pour aller plus loin, tu peux parcourir ce magazine :
- L’astronomie La géométrie de l’univers , Tangente
