Une matinée du mois de Septembre, alors que je discute avec un collègue, j’entends une impressionnante déflagration qui fait trembler les fenêtres du bureau. Grand moment de questionnement, mais qu’est-ce qui a bien pu se passer ? Un peu plus tard dans la journée, j’apprends aux informations qu’il s’agit d’un avion de chasse qui a franchi le mur du son au-dessus de la région Parisienne. Je n’aurais pas imaginé que passer le mur du son pouvait être aussi spectaculaire. Ceci m’a alors amené à m’interroger sur ce qu’est le mur du son. Je te propose dans cet article de décrire le phénomène en jeu et de le mettre en équation. C’est parti pour découvrir un autre mystère de la nature !
Définition du mur du son
On dit qu’un avion franchît le mur du son lorsque sa vitesse est supérieure à la vitesse du son. Par exemple dans l’air, la vitesse du son est d’environ 340 m/s. Ainsi, lorsque l’avion dépasse cette vitesse, un observateur au sol entend une onde de choc sous la forme d’un « bang ». Tâchons de comprendre ensemble ce qui provoque ce fameux « bang ».
Explication du « bang » supersonique
Considérons toujours l’exemple de l’avion de chasse. Lorsque l’avion vole, il émet un son qui se propage dans l’air sous forme d’ondes accoustiques dans toutes les directions. Il s’agit par exemple du son émit par les moteurs de l’avion.
Au passage d’une onde sonore émise par l’avion, l’air se comprime. Une fois l’onde passée, l’air comprimée se détend et retourne à un état d’équilibre. Cependant, lorsque l’avion vole à la vitesse du son, une accumulation d’onde se fait à l’amont de l’avion. Ceci crée alors une surpression acoustique au nez de l’aéronef.
Au delà de la vitesse du son, c’est cette surpression acoustique perçue par un observateur au sol qui est la cause du « bang » que l’on entend. Par ailleurs, le « bang » est entendu quand l’observateur (par exemple toi), se trouve à l’intérieur de ce que l’on appelle le cône de Mach. Le cône de Mach correspond à l’enveloppe des ondes sonores émises par l’avion lorsque celui-ci est en vol supersonique.
Tu l’auras bien compris, tout se joue sur la surpression de l’air au passage d’une onde sonore. Maintenant que l’on a cela à l’esprit, mettons le en équation !
Surpression acoustique
Une onde acoustique est une onde mécanique dont les vibrations sont longitudinales. Cela signifie que la vibration se fait parallèlement au sens de propagation de l’onde. Comme je te disais plus haut, en se déplaçant, l’onde comprime l’air dans lequel elle se propage. Le phénomène étant très rapide, cette transformation est considérée comme adiabatique, quasi-statique et donc la loi de LAPLACE s’applique. La loi de LAPLACE est une relation entre la pression et le volume d’un gaz parfait. Elle s’écrit de la manière suivante :
![\[ P \cdot V^{\gamma} = Constante \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-e191c1a0f974165487d773e7bfd7c964_l3.png "Rendered by QuickLaTeX.com")
Avec 
l’indice adiabatique du gaz parfait
Dans notre cas, on s’intéresse à la variation de pression de l’air provoquée par l’onde sonore. On différencie la relation de Laplace ci-dessus et on obtient :
![\[ \frac{dP}{P} + \gamma \frac{dV}{V} = 0 \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-c2ab425a2a6ed47d852b472aabd00ec4_l3.png "Rendered by QuickLaTeX.com")
Notons 
la surpression du volume d’air au passage de l’onde tel que 
. Ainsi la surpression acoustique peut s’écrire :
![\[ p = - \enspace \gamma P \frac{dV}{V} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-db79109f9cfc5e4405531b4bc2d628d0_l3.png "Rendered by QuickLaTeX.com")
Essayons d’aller un peu plus loin maintenant. Comme dans l’article sur la force centrifuge, appliquons ici la loi de Newton a un élément de volume.
Équation de propagation d’une onde sonore
Expression de la surpression acoustique
Considérons un cylindre de longueur 
et de section 
qui se situe à une position 
dans l’espace.
Maintenant, ce cylindre subit une perturbation à cause de l’onde et ses faces frontalières se déplacent de 
en et 
à la face située en 
.
Le nouveau volume du cylindre d’air est alors :
![\[\begin{align*}V &= A \cdot ( \enspace (x + dx) - x \enspace + \enspace \epsilon (x + dx,t) - \epsilon (x,t) \enspace ) \\&= A \cdot ( \enspace dx \enspace + \enspace \epsilon (x + dx,t) - \epsilon (x,t) \enspace )\\&= A \cdot dx (1 + \frac{ \partial \epsilon (x,t)}{\partial x} )\end{algin*} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-5a30d27b290892aae2b41e832286400b_l3.png "Rendered by QuickLaTeX.com")
Tu remarques ici que le premier terme de cette équation correspond au volume initial du cylindre d’air 
et, le second, à la variation de volume 
subit par le cylindre. On retrouve alors notre précédente surpression acoustique qui se réécrit :
![\[ p = - \enspace \gamma P \frac{ \partial \epsilon (x,t)}{\partial x} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-700d32820819cca29ae2e29524f1cfa5_l3.png "Rendered by QuickLaTeX.com")
Nous avons maintenant les outils en main pour appliquer le principe fondamentale de la dynamique à ce volume d’air. C’est notre prochaine étape !
Application de la loi de Newton
La symétrie du problème fait que les forces appliquées à la circonférence du cylindre s’annulent. Ainsi, notre bilan des forces se résume aux forces de pressions appliquées sur les faces et .
- La force en 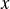s’écrit :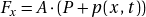
- La force en 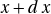s’écrit :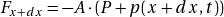
Remarque : Le force 
est de signe inverse car elle s’applique dans le sens opposé à 
dans notre convention de signe.
Notons 
la masse d’air dans le cylindre. L’équation de Newton nous dit :
![\[ \begin{align*}M \cdot \frac{d^2 \epsilon (x,t)}{dt^2} &= F_x + F_{x+dx}\\&= A \cdot (P + p(x,t)) \enspace - \enspace A \cdot (P + p(x + dx,t))\\ &= - A \cdot (p(x+dx,t) - p(x,t))\\ &= - A \cdot dx \cdot\frac{ \partial p (x,t)}{\partial x}\\&= A \cdot dx \cdot \gamma \cdot P \cdot \frac{ \partial^2 \epsilon (x,t)}{\partial x^2}\end{algin*} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-8ba4297efc49aa987383cbcd88c36a9c_l3.png "Rendered by QuickLaTeX.com")
Enfin, la masse du volume d’air peut s’écrire 
, avec 
la masse volumique de l’air. L’expression devient alors :
![\[ \frac{d^2 \epsilon (x,t)}{dt^2} = \frac{ \gamma \cdot P}{\rho} \cdot \frac{ \partial^2 \epsilon (x,t)}{\partial x^2} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-0412f51fd36a418d0bded3535ad30905_l3.png "Rendered by QuickLaTeX.com")
Ou plus communément :
![\[ \boxed{\frac{d^2 \epsilon (x,t)}{dt^2} = c^2 \cdot \frac{ \partial^2 \epsilon (x,t)}{\partial x^2}} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-bc797e7b6c1187da3f9413fc1814e7de_l3.png "Rendered by QuickLaTeX.com")
Nous y sommes ! Nous avons défini ensemble l’équation de propagation de l’onde sonore. Pour la culture, il s’agit là d’une équation de d’Alembert. Cette équation traduit la relation entre l’espace (les variables suivant ), et le temps. Il est commun en physique de rencontrer ce type de relations qui ne sont pas forcément aisées à résoudre.
Pour finir, allons encore plus vite et encore plus loin…?
Encore un nouveau phénomène à ajouter à ta besace de scientifique. Tu sais maintenant ce que représente le mur du son et, comment le mettre en équation. En effet, il existe des objets qui se déplacent plus rapidement que le son dans l’air. Mais, sais-tu qu’il n’y a pas que le mur du son qui peut être franchi… ? Et oui ! il existe des particules qui peuvent franchir le « mur de la lumière » ! Ce phénomène peut-être observé dans des réacteurs nucléaires. On appelle ce phénomène l’effet Vavilov-Tcherenkov. Cependant, ne dévoilons pas tout ici. Ce phénomène fera l’objet d’un prochain article sur Sciences Corner. D’ici là, bonne aventure dans ta quête de connaissance et à bientôt toujours au même endroit !
Pour aller plus loin sur les équations d’onde, tu peux t’orienter vers cet ouvrage :
- Lefort Ronan. Ondes et vibrations : fondamentaux et applications à l’acoustique et à la diffusion de la chaleur. Dunod
c’est pas ouf
Bonjour Burie,
Merci pour ton intérêt pour Sciences Corner.
Afin d’améliorer l’expérience de lecture, peux-tu préciser ton commentaire.
N’hésite pas à me faire tes retours directement dans le formulaire de contact.
À bientôt ! 🙂
Harry de Sciences Corner
Les avions deligne cotoient la vitesse du son : https://www.rtl.fr/actu/meteo/tempete-ciaran-des-avions-controles-a-des-vitesses-anormales-au-dessus-de-l-ocean-atlantique-7900315661