Tu as sûrement dû entendre parler de cette fameuse suite, la suite de Fibonacci. Je trouve toujours très classe de nommer cette suite, mais au fond, que vaut-elle vraiment et, pourquoi s’y intéresser. Dans cet article, je t’invite à faire tes premiers pas dans l’univers des suites mathématiques et à découvrir cette suite si populaire.
Où rencontrer cette suite ?
Mon choix s’est porté sur un exemple qui revient souvent dans les recherches internet, le nautile. Le nautile est un mollusque céphalopode possédant une coquille protectrice composée de plusieurs loges. Il est intéressant de regarder la forme en spirale de cette coquille. Et bien, il existe un lien entre la spirale du nautile et la suite de Fibonacci que je vais tâcher de t’expliquer dans cet article.
Je te propose de commencer tout d’abord par un rappel de ce qu’est une suite. Ensuite, nous sauterons à pieds joints au coeur de la résolution de la suite de Fibonacci et, comment reporter ce résultat sur le nautile.
Qu’est-ce qu’une suite ?
Une suite est le regroupement d’un ensemble de termes. Par exemple, ![]() est une suite de nombre réels. En mathématiques, on parle souvent de suite numérique, lorsqu’il y a une relation entre un terme et les termes qui le précède, on parle alors de suite récurrente. D’un autre côté, il est aussi possible d’établir une relation direct entre le terme de la suite, et sa position.
est une suite de nombre réels. En mathématiques, on parle souvent de suite numérique, lorsqu’il y a une relation entre un terme et les termes qui le précède, on parle alors de suite récurrente. D’un autre côté, il est aussi possible d’établir une relation direct entre le terme de la suite, et sa position.
Tâchons ici d’être un peu plus concret. L’expression d’une suite récurrente est telle que, pour tout entier naturel ![]() , la suite
, la suite ![]() est définie par
est définie par ![]() . Avec des mots cela signifie que, le terme
. Avec des mots cela signifie que, le terme ![]() est obtenu en fonction des termes précédents
est obtenu en fonction des termes précédents ![]() .
.
Découverte de la suite de Fibonacci
Quelle est son expression ?
La suite de Fibonacci vérifie la relation suivante :
![]()
Avec des mots cela signifie que, la valeur du terme au rang ![]() est égale à la somme des deux termes de la suite qui le précède.
est égale à la somme des deux termes de la suite qui le précède.
La suite de Fibonacci est une suite récurrente linéaire d’ordre 2 car, le terme au rang ![]() dépend des deux termes précédents. La résolution de ce type de suite se fait en passant par l’équation caractéristique.
dépend des deux termes précédents. La résolution de ce type de suite se fait en passant par l’équation caractéristique.
Sans trop tarder, voyons en quoi cela correspond.
Résolutions d’une suite récurrente linéaire d’ordre 2
Comme je le mentionnais plus haut, la résolution d’une suite récurrente linéaire d’ordre 2 peut se faire via l’équation caractéristique. À titre d’exemple, considérons un cas générale dans l’espace des réels.
À la suite…
![]()
… J’associe donc l’équation caractéristique :
![]()
Les racines du polynôme ci-dessus nous permettent alors d’exprimer l’ensemble des solutions de ![]() . Les racines du polynôme sont :
. Les racines du polynôme sont :
![]()
Ainsi, l’ensemble des solutions réelles de ![]() sont l’ensemble des fonctions vérifiant :
sont l’ensemble des fonctions vérifiant :
- Si,
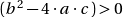 :
: ![Rendered by QuickLaTeX.com \[\forall n\in \mathbb{N} \qquad U_n \enspace = A \cdot r_1^n \enspace + B \cdot r_2^n \qquad \text{avec (A,B)} \in \mathbb{R} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-2bd30647816465bd6e6cf92312a528b8_l3.png)
- Si,
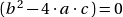 :
: ![Rendered by QuickLaTeX.com \[\forall n\in \mathbb{N} \qquad U_n \enspace = (A + B \cdot n) \cdot r^n \qquad \text{avec (A,B)} \in \mathbb{R} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-137c50ecca64633a3d2fcd36729271b2_l3.png)
- Si,
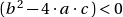 :
: ![Rendered by QuickLaTeX.com \[\forall n\in \mathbb{N} \qquad U_n \enspace = \rho^n \cdot (A \cdot cos( n \cdot \theta) \enspace + B \cdot sin( n \cdot \theta) ) \enspace \mbox{avec} \enspace (A, B, \rho, \theta) \in \mathbb{R} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-29e70fd04e715e63bdd288c1e4837974_l3.png)
Les solutions de la suite de Fibonacci
Maintenant, c’est le moment pour nous de sortir la tête du cahier et, de regarder d’un peu plus loin en quoi tous ces calculs peuvent s’appliquer à notre sujet.
Comme je disais, Fibonacci est une suite récurrente linéaire d’ordre 2. Par identification, on constate que dans notre cas, ![]() et
et ![]() . Ainsi, l’ensemble des solutions de l’équation de Fibonacci peuvent s’écrire :
. Ainsi, l’ensemble des solutions de l’équation de Fibonacci peuvent s’écrire :
![]()
Il y a beaucoup de propriétés mathématiques qui découlent de la suite de Fibonacci. Je ne pourrai malheureusement pas toutes les parcourir en long et en large. Cependant, je souhaite que l’on regarde ensemble deux points particulièrement intéressants sur ce résultat. En premier lieu, attachons nous à l’interprétation vectorielle de cette équation.
Suite de Fibonacci et les espaces vectoriels
Imagine un plan défini par deux vecteurs de base. Il est alors possible de créer n’importe quel vecteur dans ce plan par combinaison linéaire de ces deux vecteurs de base.
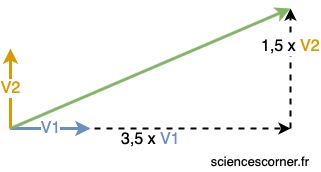
Et bien, ![]() peut être comparé au vecteur vert ci-dessus. Il s’écrit comme une combinaison linéaire des deux vecteurs de base
peut être comparé au vecteur vert ci-dessus. Il s’écrit comme une combinaison linéaire des deux vecteurs de base ![]() et
et ![]() . En somme, tous les vecteurs du plan, sont une solution de
. En somme, tous les vecteurs du plan, sont une solution de ![]() . Ce qui les différencie sont les coefficients
. Ce qui les différencie sont les coefficients ![]() et
et ![]() qui sont eux, calculés à partir des conditions initiales.
qui sont eux, calculés à partir des conditions initiales.
Un trésor presque caché
Le deuxième point que je souhaite analyser avec toi est le rapport ![]() , et plus précisément, sa valeur pour de très grandes valeurs de
, et plus précisément, sa valeur pour de très grandes valeurs de ![]() .
.
Tout d’abord, faisons une petite gymnastique mathématique pour étudier la limite du rapport ![]() . Pour ce faire, je factorise le terme
. Pour ce faire, je factorise le terme ![]() dans l’expression de
dans l’expression de ![]() .
.
![Rendered by QuickLaTeX.com \[ \forall n\in \mathbb{N}^+ \qquad F_n \enspace = ( \frac{1+ \sqrt{5}}{2})^n \cdot ( A \enspace + B \cdot (\frac{(\frac{1+ \sqrt{5}}{2}) \cdot (\frac{1- \sqrt{5}}{2})}{\frac{1+ \sqrt{5}}{2}})^n ) \qquad \text{avec (A,B)} \in \mathbb{R}^2 \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-a00c72fb5644ad2c46780064c3b5cb2a_l3.png)
On reconnait alors une identité remarquable qui nous permet de simplifier l’équation :
![Rendered by QuickLaTeX.com \[ \begin{align*}(\frac{1+ \sqrt{5}}{2}) \cdot (\frac{1- \sqrt{5}}{2}) &= \frac{1}{2}^2 - \frac{\sqrt{5}}{2}^2 \\&= -1 \end{algin*}\]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-37ed41be19db5f573d6e8c237f5f4007_l3.png)
Par conséquent, si je note ![]() , l’expression de
, l’expression de ![]() se simplifie de la manière suivante :
se simplifie de la manière suivante :
![]()
Remarquons que ![]() et donc, lorsque
et donc, lorsque ![]() tend vers l’infini, on obtient :
tend vers l’infini, on obtient :
![]()
Partant de ce résultat, pour de très grandes valeurs de ![]() , le rapport
, le rapport ![]() équivaut à
équivaut à ![]() , et donc :
, et donc :
![Rendered by QuickLaTeX.com \[ \text{pour n très grand} \qquad \boxed{\frac{F_n+1}{F_n} = \frac{1+ \sqrt{5}}{2}} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-2186ea56a370ad7a56a85174e577a481_l3.png)
Ta pioche de chercheur vient de taper sur un nombre bien connu en mathématique. Il s’agit du nombre d’Or. Je t’invite à garder ce nombre à l’esprit. Nous découvrirons ensemble à quoi il correspond dans un prochain article.
Résumons le deuxième point. Un fait remarquable de la suite de Fibonnaci est que, le taux d’accroissement de cette suite, pour des ![]() très grands, tend vers le précieux nombre d’Or.
très grands, tend vers le précieux nombre d’Or.
La suite de Fibonacci et le nautile
Tracé de spirale à partir de la suite
Intéressons nous à quelques valeurs de la suite de Fibonacci :
Maintenant, pour chaque terme de la suite, je vais dessiner un carré dont le côté est égale à la valeur du terme. Concrètement, pour ![]() , je dessine un carré de côté 1. Pour
, je dessine un carré de côté 1. Pour ![]() , je dessine une carré de côté 1. Pour
, je dessine une carré de côté 1. Pour ![]() , je dessine une carré de côté 2, et ainsi de suite jusqu’a
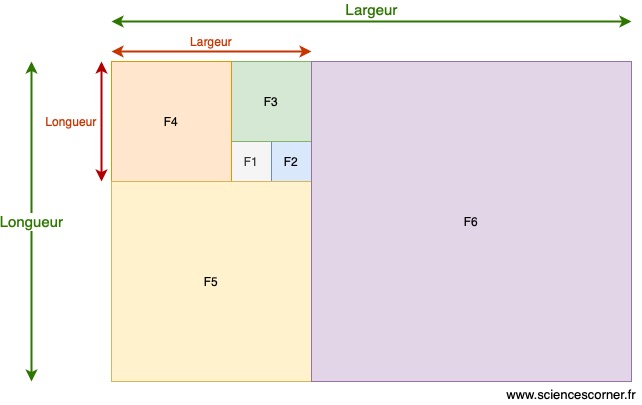
, je dessine une carré de côté 2, et ainsi de suite jusqu’a ![]() . Ensuite, je positionne côte à côte les carrés, de sorte que l’ensemble forme un rectangle. Le résultat est le suivant :
. Ensuite, je positionne côte à côte les carrés, de sorte que l’ensemble forme un rectangle. Le résultat est le suivant :

Pour finir, je trace un quart de cercle dans chaque carré. Chaque quart de cercle est tangent aux deux extrémités des carrés ![]() et
et ![]() , le tracé obtenu est alors continu. On peut alors apercevoir une magnifique forme de spirale !
, le tracé obtenu est alors continu. On peut alors apercevoir une magnifique forme de spirale !
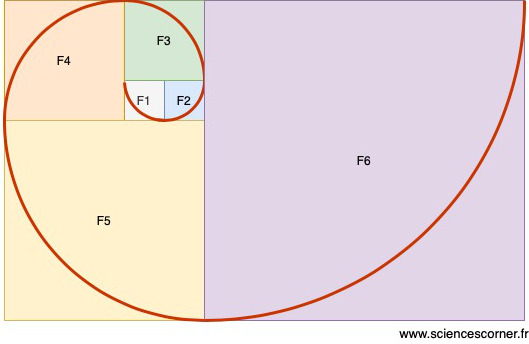
Rappelle toi le deuxième point souligné précédemment. Nous avons vu que pour de grandes valeurs de ![]() , le taux d’accroissement de la suite de Fibonacci tend vers le nombre d’Or. Ainsi, la spirale obtenue grâce à la suite de Fibonacci elle aussi tend vers la spirale d’Or !
, le taux d’accroissement de la suite de Fibonacci tend vers le nombre d’Or. Ainsi, la spirale obtenue grâce à la suite de Fibonacci elle aussi tend vers la spirale d’Or !
La spirale d’Or est la courbe obtenue dans le cas où dans chaque rectangle, le rapport ![]() , c’est à dire le nombre d’Or précédemment calculé.
, c’est à dire le nombre d’Or précédemment calculé.
En somme, la suite de Fibonacci permet d’avoir une bonne approximation de la spirale d’Or. Mais qu’en est-il de notre fameux nautile ? La réponse est juste en dessous.
Le nautile et la spirale logarithmique
La forme de la coquille du nautile, tout comme la spirale d’Or, sont des spirales logarithmiques. L’expression mathématique d’une telle spirale est la suivante :
![]()
![]() correspond à la distance d’un point de la spirale, par rapport au centre de la spirale.
correspond à la distance d’un point de la spirale, par rapport au centre de la spirale.
Le coefficient ![]() de cette équation est l’élément qui différencie la forme de chaque spirale logarithmique. Le coefficient
de cette équation est l’élément qui différencie la forme de chaque spirale logarithmique. Le coefficient ![]() permet, quant à lui, de positionner la spirale par rapport à son centre de rotation. De ce fait, si la forme spiralée du nautile est bien celle d’une spirale d’Or, alors leurs coefficients
permet, quant à lui, de positionner la spirale par rapport à son centre de rotation. De ce fait, si la forme spiralée du nautile est bien celle d’une spirale d’Or, alors leurs coefficients ![]() sont les mêmes. Vérifions le en calculant ce coefficient
sont les mêmes. Vérifions le en calculant ce coefficient ![]() .
.
Calcul du paramètre b de la spirale du nautile
Tout d’abord, notons que la spirale d’Or est un cas particulier de spirale logarithmique. Elle vérifie la relation suivante : Si, j’agrandie la spirale d’un facteur ![]() (nombre d’or), et si je tourne la nouvelle spirale obtenue d’un quart de tour ( soit
(nombre d’or), et si je tourne la nouvelle spirale obtenue d’un quart de tour ( soit ![]() ), alors la nouvelle spirale obtenue se superpose sur l’ancienne.
), alors la nouvelle spirale obtenue se superpose sur l’ancienne.
En d’autre terme :
![]()
A partir de cette égalité, on trouve que, dans une spirale d’Or, le paramètre ![]() est tel que
est tel que ![]() . Ainsi, l’expression de la spirale d’Or s’écrit :
. Ainsi, l’expression de la spirale d’Or s’écrit :
![]()
Afin de faire le lien entre le nautile et le paramètre ![]() de sa spirale, intéressons nous au rapport
de sa spirale, intéressons nous au rapport ![]() . Ce rapport correspond au rapport de rayon entre deux points de la spirale, séparés d’un tour. On trouve, par calcul, dans le cas d’une spirale d’Or, le résultat suivant :
. Ce rapport correspond au rapport de rayon entre deux points de la spirale, séparés d’un tour. On trouve, par calcul, dans le cas d’une spirale d’Or, le résultat suivant :
![]()
Vérifions à partir d’une photo du nautile que l’on trouve un résultat proche de celui ci. Pour ce faire, je mesure premièrement le rayon d’un point quelconque ![]() , puis
, puis ![]() . Ensuite, je fais le rapport des deux.
. Ensuite, je fais le rapport des deux.
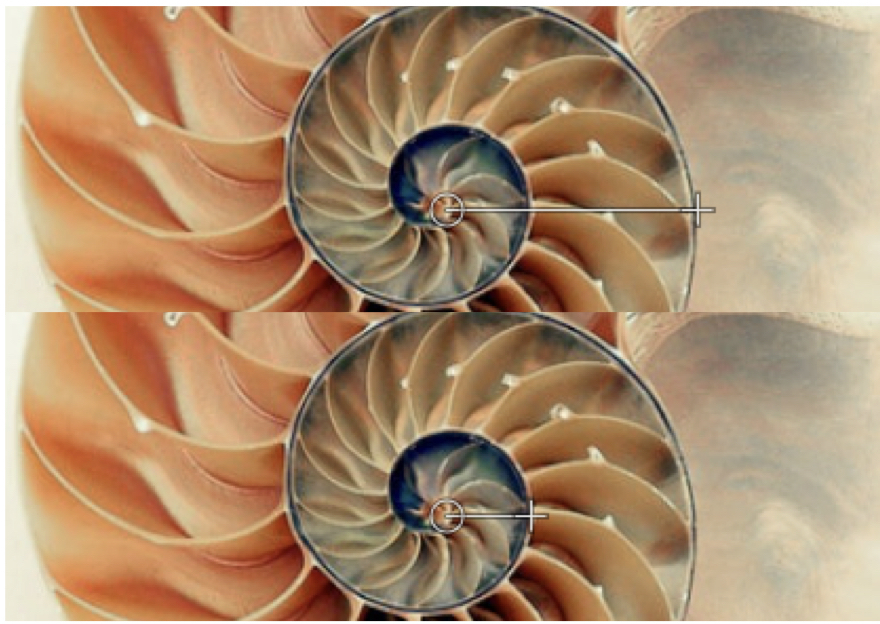
Je trouve, pour cette photo de nautile, et de manière approximative, un rapport qui vaut ![]() . En revanche, pour une spirale d’Or, ce rapport vaut
. En revanche, pour une spirale d’Or, ce rapport vaut ![]() . Ces deux rapports sont très différents. Nous pouvons alors dire que, la spirale du nautile n’est pas une spirale d’Or.
. Ces deux rapports sont très différents. Nous pouvons alors dire que, la spirale du nautile n’est pas une spirale d’Or.
En conclusion
La suite de Fibonacci est une suite linéaire récurrente d’ordre 2 dont, le taux d’accroissement tend vers le nombre d’Or. La spirale obtenue à partir de la suite de Fibonacci donne une bonne approximation de la spirale d’Or. Le lien entre la spirale d’Or et la forme en spirale du nautile réside dans le fait qu’elles sont toutes deux des spirales logarithmiques. Cependant, il n’est pas possible de dire que la spirale du nautile est une spirale d’Or. En effet, le paramètre définissant la forme de la spirale du nautile est bien différent de celui de la spirale d’Or.
Notre aventure d’aujourd’hui s’arrête ici mais notre expédition n’est pas terminée. Il y a encore tellement de choses à découvrir. Je te donne donc rendez-vous sur Sciences Corner pour une toute nouvelle expédition sur notre belle planète Terre !
As-tu toi aussi rencontré des spirales logarithmiques autour de toi ? Sont-elles des spirales d’Or ? Partage moi tes découvertes en commentaire !
Pour aller plus loin, tu peux également parcourir ces différentes ressources :
- Rousseau, C ( 2008). Nautile, nombre d’or et spirale dorée. http://accromath.uqam.ca. Consulté le 18 Mai 2020 sur http://accromath.uqam.ca/accro/wp-content/uploads/2013/04/nautile.pdf
- Ferréol, R (2013). Spirale d’or, spirale de Fibonacci et spirales naturelles. mathcurve.com. Consulté le 18 Mai 2020 sur https://mathcurve.com/courbes2d/logarithmic/spiraledor.shtml
