Tu as certainement remarqué que l’écoulement de l’eau que tu verses dans un verre est différent de celui du miel que tu étales sur une tartine. Cette différence d’écoulement est notamment due à une propriété des liquides que l’on appelle la viscosité. Cette propriété des matériaux n’a pas échappé aux scientifiques qui ont cherché à modéliser cette notion de viscosité dans les matériaux. Aujourd’hui, sur Sciences Corner, je ne vais pas t’apprendre à calculer le temps que va prendre ton miel pour s’étendre sur ta tartine, quoi que la réflexion pourrait être intéressante. Non, aujourd’hui nous irons encore plus loin. Nous découvrirons comment modéliser un matériau viscoélastique ! Comme cas d’application, je te propose de définir le modèle du solide de Kelvin-Voigt.
Viscosité et viscoélasticité, quelle est la différence ?
Si les mots viscosité et viscoélasticité se ressemblent autant, c’est parce qu’il existe un réel lien entre ces deux notions. Cependant, prenons le temps de les comprendre individuellement. Tout d’abord, la viscosité.
La viscosité
La viscosité est une propriété qui est liée aux frottements internes dans les fluides. Pour mieux l’interpréter, prenons l’exemple d’un fluide contenu entre deux plaques parallèles. Si ça peut t’aider à le visualiser, imagine le miel sur ta tartine en bas, et en haut, ton couteau avec lequel tu vas étaler le miel. La plaque du dessus, ici ton couteau, est animée par un mouvement de translation et l’autre plaque, la tartine, est fixe. La plaque mobile aura alors tendance à entrainer les couches de fluides alors que la plaque fixe elle, tend à les retenir. Il en résulte alors des forces de frottement qui s’exercent tangentiellement sur chaque couche du fluide. Ces forces tangentielles sont appelées forces de cisaillement.
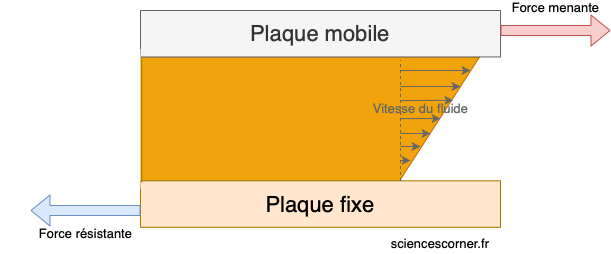
Finalement, la viscosité se traduit par l’aptitude du fluide à s’opposer au cisaillement dans le fluide. Ainsi, à partir de cette définition on peut en déduire que la viscosité du miel est plus grande que celle de l’eau car il s’écoule moins facilement que l’eau. Pour donner des ordres de grandeur, la viscosité dynamique de l’eau à 20°C est de 
,alors que celle du miel est de 
.
La viscoélasticité et le solide de Kelvin-Voigt
La viscoélasticité, quant à elle, est une propriété des matériaux qui reprend en tout, les caractéristiques d’un liquide visqueux, mais à cela s’ajoute les propriétés du solide élastique. En d’autre termes, la viscoélasticité est l’état intermédiaire entre un liquide visqueux et un solide élastique parfait.
Le solide de Kelvin-Voigt, par exemple, est un modèle de matériau viscoélastique. Ainsi, il partage à la fois les propriétés d’un liquide visqueux, mais aussi du solide élastique.
Il est temps maintenant de mettre la main dans les équations et d’écrire ce modèle. Tout d’abord, je te propose d’établir les équations rhéologiques de ces deux états, liquide visqueux et solide élastique. Mais, sais-tu ce qu’est la rhéologie ? Pas de panique, je t’explique.
Équation rhéologique, viscosité et viscoélasticité
Équation rhéologique du solide élastique parfait
Afin de faciliter la compréhension du sujet, je m’intéresse au cas particulier des mouvements de cisaillement simple.
La rhéologie est la science qui étudie la déformation et le mouvement de matière sous l’application d’une contrainte. Ainsi, en rhéologie, il existe une équation qui relie les contraintes aux déformations.
![\[ \varepsilon = f ( \tau ) \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-e852cefb9ba93bb1706bc681cd45788d_l3.png "Rendered by QuickLaTeX.com")
Où :
Dans le cas du solide élastique parfait, l’équation rhéologique en jeu est traduite par la 
:
![\[ \varepsilon (t) = J \cdot \tau(t) \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-ab612141a3e404f1a971b7de2652b6c5_l3.png "Rendered by QuickLaTeX.com")
Où :
Remarquons un élément important dans cette relation. L’équation nous dit que, si une contrainte est appliquée au solide, alors instantanément ce solide se déforme proportionnellement à la contrainte appliquée.
Il est alors commun en rhéologie de modéliser le solide élastique parfait par un ressort .
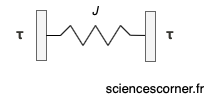
Équation rhéologique du liquide visqueux newtonien
Pour bien comprendre cette équation, il est nécessaire de se rappeler de la définition de la viscosité. Pour rappel, la viscosité est l’aptitude à s’opposer au cisaillement dans le fluide. Dans le cas du liquide visqueux newtonien, la relation entre contrainte et déformation est une loi linéaire entre les contraintes dans le fluide et la vitesse de déformation dans le fluide :
![\[ \frac{d \varepsilon (t)}{dt} = \frac{\tau(t)}{\eta} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-78f19944a419e53a59653e6622f78b2e_l3.png "Rendered by QuickLaTeX.com")
Où :
À ce stade, il est intéressant que tu remarques deux propriétés que je trouve fort remarquables. La première, c’est qu’un liquide visqueux newtonien se souvient de toutes les contraintes qu’il a subit. Pour t’en convaincre, intégrons cette équation. On obtient alors :
![\[ \varepsilon (t) = \frac{1}{\eta} \int_{0}^{t} \tau(t) dt \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-ee95c66e077514b65f624b283fc4d9d4_l3.png "Rendered by QuickLaTeX.com")
Ainsi, on constate ici que la valeur de la déformation 
, tient compte de toutes les précédentes contraintes qui ont été appliquées dans le fluide.
Le deuxième point tout aussi important à remarquer est que, si la contrainte est ramenée à 0, alors la déformation subie par le fluide reste constante mais à la valeur de déformation qu’elle possédait. En quelques mots, la déformation subie par le fluide est irréversible.
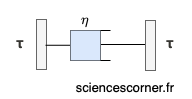
En rhéologie, il est commun de représenter le liquide visqueux newtonien par un amortisseur de coefficient de viscosité 
:
Nous sommes maintenant bien armé pour établir le modèle de Kelvin-Voigt. Ne perdons pas un instant !
Le solide de Kelvin-Voigt
Nous y sommes enfin, cependant tu as peut-être perdu la feuille de route avec toute cette théorie. Prenons deux secondes pour nous rafraîchir l’esprit.
Le solide de Kelvin-Voigt est une modélisation d’un solide viscoélastique. La viscoélasticité correspond à l’état l’intermédiaire entre un solide élastique et un liquide visqueux. Ainsi, nous avons défini ces deux états afin d’en déduire le modèle du solide de Kelvin-Voigt qui est :
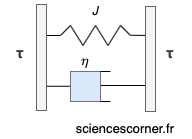
A partir de nos précédentes définitions, on peut alors déterminer l’équation rhéologique du solide de Kelvin-Voigt.
![\[ \tau_1(t) = \frac{1}{J}\varepsilon_1 (t) \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-5eca403a6e459ad93a00a925aee55fc1_l3.png "Rendered by QuickLaTeX.com")
![\[ \tau_2(t) = \eta \cdot \frac{d \varepsilon_2 (t)}{dt} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-1a7500617167c83872ae533955abe733_l3.png "Rendered by QuickLaTeX.com")
Ensuite, en s’appuyant sur les lois d’associations en parallèle, on sait que :
![\[ \varepsilon_1 = \varepsilon_2 \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-1a37bb5c1b9022ed3ff626b98e25c360_l3.png "Rendered by QuickLaTeX.com")
![\[ \tau (t) = \tau_1(t) + \tau_1(t) \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-c92fb1c2be16c5c9e7fcf2883a76b7c3_l3.png "Rendered by QuickLaTeX.com")
En obtient alors une équation différentielle du premier ordre en 
:
![\[ \eta \cdot \frac{d \varepsilon (t)}{dt} + \frac{1}{J}\varepsilon (t) = \tau (t) \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-56d43a13f85e3d983c2f9f5146d50e8c_l3.png "Rendered by QuickLaTeX.com")
Ça y est nous y sommes ! enfin presque… L’équation ci-dessus traduit la relation qui existe entre les contraintes et les déformations dans le cas du solide de Kelvin-Voigt. Bon, on ne va quand même pas s’arrêter là ? Parce que en l’état, je ne sais pas trop quoi en faire. Pour achever complètement notre modélisation, je t’invite à écrire la fonction 
de ce solide.
Fonction fluage du solide de Kelvin-Voigt
La fonction fluage correspond à la déformation subie par un matériau lorsqu’il est soumis à une contrainte unitaire et, que cette contrainte est maintenue constante. Chaque matériau possède sa propre fonction fluage.
Plus concrètement, dans la relation établie précédemment, on va noter 
. On obtient alors :
![\[ \eta \cdot \frac{d f (t)}{dt} + \frac{1}{J}f (t) = 1 \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-21b383a4d8336ddc7fcfaec032ebd12e_l3.png "Rendered by QuickLaTeX.com")
Tu l’as reconnu, il s’agît d’une équation différentielle d’ordre 1 à coefficient constant. Les solutions d’une équation de ce type sont connues et, on aboutit alors à la fonction fluage du solide de Kelvin-Voigt :
![\[ \boxed{f (t) = J \cdot ( 1 - e^{ -t / \theta}) } \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-f1dd453b74eb4484a35b9f3ea8b84507_l3.png "Rendered by QuickLaTeX.com")
Avec :
On y est, nous avons réussi à établir cette équation rhéologie du solide. Prenons maintenant le temps de la comprendre. Souviens toi, je t’ai souligné des points clés concernant le solide élastique parfait et sur les liquides visqueux. Et bien, regardons ce qu’il en est lorsque l’on trace les courbes de fluage :
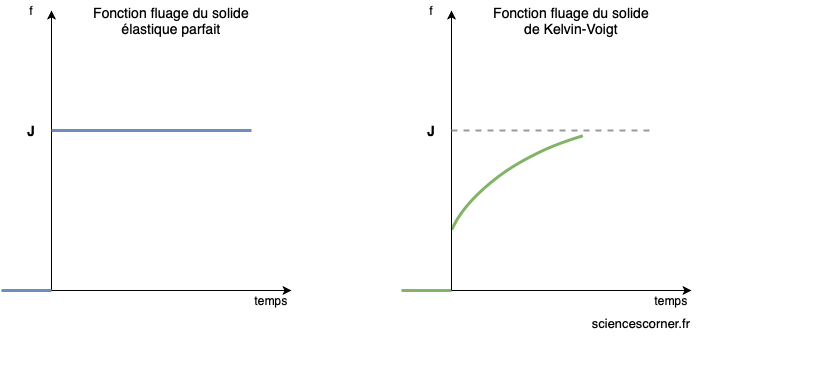
On constate que contrairement au solide élastique parfait, la déformation du solide viscoélastique n’est pas instantanée. Cette déformation est retardée par la présence du caractère visqueux dans le solide Ainsi, on dit que le solide de Kelvin-Voigt a une élasticité retardée. Voilà, maintenant tu sais tout de ce modèle.
Le mot de la fin : un modèle peut en cacher un autre…
Eh bien oui ! Nous sommes arrivés au bout de la modélisation du solide de Kelvin-Voigt. Tu l’auras bien compris, il s’agît d’un modèle viscoélastique qui permet, en rhéologie, de définir le comportement d’un matériau. Dans notre cas, le solide de Kelvin-Voigt est l’association en parallèle d’un solide élastique parfait et d’un liquide visqueux newtonien. Mais, si on associait un solide élastique parfait et un liquide visqueux newtonien en série, qu’est-ce que l’on obtiendrait ? Un indice ? Un liquide de Maxwell ! Tu l’auras compris, nous avons tout juste aperçu l’ensemble des modèles possibles en viscoélasticité. Mais nous avons encore beaucoup à apprendre sur notre monde. C’est ici que je te dis à bientôt pour de nouvelle découverte sur Sciences Corner.
Tu veux en connaître plus sur les modèles viscoélastiques ? Peut-être même le modèle du liquide de Maxwell ? Voilà une référence qui t’aidera à trouver ton bonheur :
- Guy Couarraze et Jean-Louis Grossiord. Initiation à la rhéologie. Tec&Doc
Que ce soit en fluage ou en relaxation de contrainte, la reponse a une sollicitation d’un materiau viscoelastique depend du temps (ou de la frequence, lors d’experiences dynamiques). Ce n’est pas le cas pour un materiau purement elastique. Soumis a une contrainte (ou a une deformation ) constante, le comportement liquide est caracterise par un ecoulement visqueux. Differents modeles permettent de decrire la viscoelasticite lineaire. Le modele de Maxwell est adapte au liquide viscoelastique. Le modele de Kelvin-Voigt quant a lui est un modele elementaire de solide viscoelastique. Il existe egalement respectivement pour ces deux cas le modele de Zener et celui de Burgers .
Bonjour !
Merci pour ton commentaire et ces précisions 🙂