Pour nos amis de classe préparatoire cette inégalité doit rappeler de beaux souvenirs de khôlle, n’est-ce pas ? J’ai encore en tête des sujets de Math où la fameuse inégalité de Cauchy-Schwarz était la clé pour débloquer les problèmes tous tout aussi abstraits les uns que les autres. Récemment, et de manière plutôt inattendue, l’inégalité de Cauchy-Schwarz m’a à nouveau solutionnée un problème qui n’était pourtant pas gagné d’avance. Mais cette fois, c’était pour une application beaucoup plus concrète. Je te propose au travers d’un cas pratique, de découvrir ou redécouvrir l’inégalité de Cauchy-Schwarz.
L’inégalité de Cauchy-Schwarz dans un cas pratique
Un peu de contexte pour débuter
Considérons le cas d’un système d’aération d’un bâtiment. L’air circule au travers de canalisations séparées par des grilles. Supposons que les grilles du système de ventilation soient à peu près circulaires. Pour garantir une bonne aération du bâtiment, il faut s’assurer que le débit d’air qui circule est suffisant. Cependant, les grilles peuvent s’encrasser et diminuer le débit d’air qui sert à aérer le bâtiment.
D’après les concepteurs du système de ventilation, pour assurer une bonne aération du bâtiment, la section de passage totale au travers des grilles doit être supérieure à une section de passage d’air minimale.
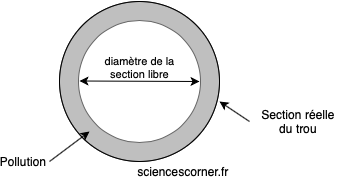
Maintenant, considérons que la grille possède 
trous. Alors, la section totale de passage d’air de la grille vaut :
![\[ \begin{align*}S_{totale} &= \sum_{i=1}^{n} S_{trou}\\&= \sum_{i=1}^{n} \frac{ \pi D^2_i}{4}\\&= \frac{ \pi}{4} \ \sum_{i=1}^{n} D^2_i\\\end{algin*} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-df7830cbde7a279e76f095b2114aa0e2_l3.png "Rendered by QuickLaTeX.com")
Cependant, cette expression du besoin est plutôt compliquée pour un contrôleur. Afin de faciliter l’inspection, le contrôleur préfèrera considérer le diamètre moyen de l’ensemble des trous de la grille. Par cette approche, la section d’air traversant la grille, que je noterai 
vaut :
![\[\begin{align*}S_{moyen} &= n \ \pi \ \frac{ D_{moyen}^2 }{4}\\&= n \ \frac{ \pi}{4} \ (\frac{ 1}{n} \ \sum_{i=1}^{n} D_i )^2\\&= \frac{ 1}{n} \ \frac{ \pi}{4} \ (\sum_{i=1}^{n} D_i)^2 \end{algin*} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-3262c17fdaa64269caed7e04cd9a222b_l3.png "Rendered by QuickLaTeX.com")
Maintenant, notre travail consiste à prouver qu’à chaque instant, est inférieure à 
.
![\[ S_{moyen} \ \leq \ S_{totale} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-e99ce81c236b6ddaf09dad13aad72fc4_l3.png "Rendered by QuickLaTeX.com")
C’est à dire :
![\[ \frac{ 1}{n} \ (\sum_{i=1}^{n} D_i)^2 \leq \ \sum_{i=1}^{n} D^2_i \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-e1b0fbfaaf2c6dd7d36439f151ae333a_l3.png "Rendered by QuickLaTeX.com")
Si cette inégalité n’est pas vérifiée, alors cela signifie qu’il existe des cas où l’inspecteur peut affirmer que la ventilation du bâtiment est correcte alors que ce n’est pas le cas.
Derrière cette inéquation se cache l’incontournable inégalité de Cauchy Schwarz. Tu l’as identifiée ? Si la réponse est non alors pas d’inquiétude, je te la mets en lumière.
Définition de l’inégalité de Cauchy Schwarz
L’inégalité de Cauchy-Schwarz s’applique dans un espace préhilbertien, c’est à dire dans un espace vectoriel muni du produit scalaire. L’énoncé de l’inégalité de Cauchy-Schwarz est le suivant :
Le produit scalaire entre deux vecteurs est inférieur ou égale au produit des normes de ces deux vecteurs, c’est à dire :
![\[ \mid < x,y> \mid \enspace \leq \enspace \parallel x \parallel \ \parallel y \parallel \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-5412177f98f222db944c0c78932a8b62_l3.png "Rendered by QuickLaTeX.com")
Il existe divers espaces préhilbertiens. Par exemple, l’espace constitué de matrices carrées d’ordre 4, ou encore l’espace constitué de fonctions continues dans l’intervalle ![[-1 ; 1]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-156941962ec95c9b4c8d8ad5ad509840_l3.png "Rendered by QuickLaTeX.com")
sont des espaces préhilbertiens dont les vecteurs x et y sont respectivement des matrices ou des vecteurs.
De la théorie à la pratique
L’astuce dans notre cas consiste à choisir un produit scalaire particulier de l’espace vectoriel 
. Le produit scalaire considéré est le suivant :
![\[ \mid < x,y> \mid \enspace = \enspace \sum_{i=1}^{n} x_i y_i \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-50f1c2412afbc2ae0faeda9c71d7dd1e_l3.png "Rendered by QuickLaTeX.com")
Par définition on peut alors écrire la norme d’un vecteur à partir de l’expression de ce produit scalaire :
![\[ \parallel x \parallel \ = \sqrt{\mid < x,x> \mid} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-299b844d4410dcb21a8176c2c5f4d2ec_l3.png "Rendered by QuickLaTeX.com")
Maintenant que nous connaissons toutes ces définitions, je te propose de regarder ce que devient l’inégalité de Cauchy Schwarz en remplaçant chaque terme par son expression. On obtient alors :
![\[ \sum_{i=1}^{n} x_i y_i \enspace \leq \enspace \sqrt{ \sum_{i=1}^{n} x_i^2} \ \sqrt {\sum_{i=1}^{n} y_i^2} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-7c6506b216ac143e22152ac1e1606c20_l3.png "Rendered by QuickLaTeX.com")
Nous ne sommes plus très loin de notre objectif maintenant. La dernière astuce consiste à dire que l’un de nos vecteurs par exemple x vaut : 
. Ceci est possible car 
Notre précédente inégalité devient alors :
![\[ \sum_{i=1}^{n}y_i \enspace \leq \enspace \sqrt{ \sum_{i=1}^{n} 1} \ \sqrt {\sum_{i=1}^{n} y_i^2} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-b13635ee5025a223a82ed2dbb9faecb3_l3.png "Rendered by QuickLaTeX.com")
Soit :
![\[ \sum_{i=1}^{n}y_i \enspace \leq \enspace \sqrt{n} \ \sqrt {\sum_{i=1}^{n} y_i^2} \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-f2d6f492d9e6c1299eb0987d04368d5f_l3.png "Rendered by QuickLaTeX.com")
Afin de s’affranchir de la racine carré dans notre inégalité, on passe les deux termes au carré, ce qui ne modifie pas le sens de l’inégalité car ces termes sont tous deux positifs. En considérant n strictement positif, on obtient alors :
![\[ (\sum_{i=1}^{n}y_i )^2 \enspace \leq \enspace n \ \sum_{i=1}^{n} y_i^2 \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-42cacdb1feb2d5138817471c36b6c0c8_l3.png "Rendered by QuickLaTeX.com")
Soit, en divisant par n:
![\[ \frac{1}{n} (\sum_{i=1}^{n}y_i )^2 \enspace \leq \enspace \sum_{i=1}^{n} y_i^2 \]](https://sciencescorner.fr/wp-content/ql-cache/quicklatex.com-b47ff7d83dcc976a8ddd4cd371da30fd_l3.png "Rendered by QuickLaTeX.com")
Ça y est, nous y sommes ! En remplaçant 
par la lettre 
, nous retombons exactement sur l’inégalité que l’on souhaite démontrer. Tu remarqueras que est bien strictement positif car il s’agit du nombre de trous dans la grille de ventilation.
En résumé
L’inégalité de Cauchy-Schwarz peut être appliquée dans différentes situations de notre quotidien dès lors que l’espace vectoriel et le produit scalaire qui s’y applique sont correctement identifiés. Une fois ces fondamentaux établis, il est alors possible de choisir astucieusement la valeur de l’objet mathématique qui permettra d’atteindre son objectif. Si tu as bien compris le fonctionnement de cette inégalité, c’est maintenant à toi de jouer. Partages avec nous tes cas d’applications de l’inégalité de Cauchy Schwarz dans la vie de tous les jours. N’hésites pas à être imaginatif, cette inégalité peut se cacher là où on s’y attend le moins ! Dans l’attente de lire tes découvertes, je te dis à bientôt sur Sciences Corner !
